前言
現今是一個知識型社會,而本港學校亦重視「專科專教」的問題,希望教師能有效地幫助學生在不同學科上建構正確的知識。正如諾貝爾文學獎得主蕭伯納( George Bernard Shaw) 就知識所說過的一句名言:
“False knowledge is even more dangerous than ignorance.”(「錯誤的知識比無知更危險。」)
因此,教師的知識對學生有極深的影響。
教師知識的分類
上世紀 70 年代,英國倫敦大學教育學院〔University of London Institute of Education( 1971)〕就師資培訓提出兩個普遍的觀點:
1. 教師需受訓,但不必有高深的學問。(Teachers should be trained but need not be educated.)
2. 教師需有高深的學問,但不必受訓。(Teachers should be educated but need not be trained.)
由此可見,當時社會人士認為教師的知識領域包括兩個層面,即專科知識和專業知識,雖然哪種知識對教師來說較重要並沒有一致的看法。
那麼,現時教育界怎樣劃分現代教師的知識領域呢?當今研究教師知識的著名學者美國哈佛大學教授 Lee Shulman( 1987)列出現代教師應有的七大知識類別:
1. 專科的知識( content knowledge)
2. 一般的教學知識,即核心教學方法和原理,如課室管理( general pedagogical knowledge)
3. 課程知識( curriculum knowledge)
4. 專科的教學知識,即專科教師的獨有專業知識,如小學生有多少種進行多位整數加/ 減計算的方法、小學生可怎樣理解分數的除法計算、小學生應怎樣認識圓周率的歷史背景和發展等(pedagogical content knowledge)
5. 有關學習者及其特性的知識,如學童在不同發展階段的心理學( knowledge of learners and their characteristics)
6. 有關教育情境的知識,如學校至教育體系的架構和管理、教育經費的分配、學校社區的文化等( knowledge of educational contexts)
7. 有關教育哲學和歷史的知識,如教育的目標、教育的價值觀等( knowledge of educational aimsand values, their philosophical and historical grounds)
從Lee Shulman 教授所提出有關教師知識的七種分類,亦可見教師的知識領域有兩大類:
1. 專科知識( 種類 1、3 和 4)—— 與教師教授的科目有關;
2. 專業知識( 種類2、5、6和7)—— 與教師教授的科目無關,而是一些通用的教育知識、教學原理和技能。
教師的專科知識相對於教師的專業知識
在第二次世界大戰前後,教師的資歷較注重於他們的專科知識。例如 Lee Shulman( 1986)教授在檢視上世紀美國一些州、縣的教育部門周年報告時,發現教師註冊的考核中,在1000 分滿分中,其中950 分是測考教師任教的專科知識,而僅有50 分是與教學有關的專業知識。
在 1970 至 1990 年代,教育研究﹝例如 Berliner and Rosenshine( 1977), Rosenshine and Stevens( 1986)﹞較集中於教師的專業知識,認為有效的通用教學技能如課室管理、善用評估資料、對學生的正面回饋等,是促進學生有效學習的主要因素,而教師的專科知識被視為次要。當時有大量學術研究描述,探究和分析學與教的過程,視它們為與學科內容無關的一般、共通活動。但 McNamara( 1991) 指出這些研究忽略了課堂的實質組成部分,即教師教授的學科知識。
從1990 年代開始,教育學者重新強調及重視教師專科知識的重要性。現時的觀點是教師的專科知識和專業知識同樣重要,缺一不可。此外,教師的專科知識不應只注重科目知識內容(contents) 的掌握,亦需重視科目知識的建構過程( processes)。
就小學數學科而言,還有另一個需關注的理由,因為很多教育決策者及一般社會人士認為小學的數學知識較淺易,任何教師只要能掌握基本的算術運算、認識常用的度量單位和公式、分辨不同的幾何圖形等,都能有效教授小學數學科。但 Ball( 1990) 的研究顯示受訓的小學準教師的數學理解和體驗趨於表面和侷限於法則( rule-bound)。Duckworth( 1987) 以實例展示小學數學的深度和複雜性;而 Lampert( 1986) 則以乘法為例解說小學數學課程內,看似簡易的內容背後的數學複雜性。近年有相當多研究﹝例如 Ma( 1999), Martin and Harel( 1989), Fung( 1999), Post( 1988))﹞顯示部分現職及受訓的小學數學科教師未能掌握現時小學數學課程內的知識建構過程( processes),對一些基本數學概念亦缺少透徹的認識和理解。
教師專科知識的分類
Lee Shulman( 1986) 教授再把教師的專科知識分為三大類:
1. 學科知識( subject matter content knowledge)
2. 專科的教學知識( pedagogical content knowledge)
3. 課程知識( curriculum knowledge)
讓我們較詳細理解以上三類的教師專科知識。
1. 學科知識( subject matter content knowledge) -
上世紀的著名教育家杜威﹝John Dewey( 1904/1964)﹞認為「施教的行為諸如講解、提供論證等是不能和學科知識分割的,需要教師的學科知識為後盾」。英國劍橋大學的Rowland et al(2009) 的研究說明小學數學教師的學科知識水平對他們的課堂教學表現有極深的影響。小學數學科教師在課堂上的自信心、他們所採用的教學策略、他們的提問方法和問題素質、師生互動的頻次和質素等都受制於他們的學科知識水平。正如 Ball( 1990) 的研究所說,學科知識水平低的教師的課堂教學流於表面和侷限於法則( rule-bound)。
現時數學教師所必須掌握的知識問題,是各國教師教育研究機構和教師培訓學者所關心和討論的熱點。曾任職於中文大學教育學院的黃毅英教授(2012) 在所撰《數學教師不怕被學生難倒了:中小學數學教師所需的數學知識》一書內,詳盡地論述了中小學數學教師所需的數學知識,值得本地的數學科教師細讀。
2. 專科的教學知識( pedagogical content knowledge) -
專科的教學知識除了包括本科的不同學習心理學、教學法和評估方法外,還有學科內概念的不同表象( representations),概念和原理的不同比喻、範例、解釋和示範,學生常有的誤解和先入為主的想法,掌握和理解不同學生就學習某課題時可能面對的困難,等等。
專科的教學知識和學科知識有所不同。就以多位整數的加/ 減運算來說,學科知識多關注加/ 減運算的意義,兩者的關係和相關的性質,如交換、結合性質;但專科的教學知識則涉及學童可怎樣進行多位整數的加 / 減運算,直式( column method) 的運算方法與其它加 / 減運算策略的優、劣比較,各國教育體系和數學教育學者對這課題的不同看法和建議等。例如荷蘭推行的「現實數學教育」[Realistic Mathematics Education( RME)] 運動在計算方法的教學上引入了一些根本性的改變。van den Heuvel(2001) 概述了 RME 內的建議,主張應先以心算方法為重點,然後才發展不同層次的筆算方法,而筆算方法不應只侷限於直式。Beishuizen(2001) 闡釋了RME 的取向是讓學童「透過互動的教學來解決各式現實生活中的問題,而不是直接地教授標準計算程序」。
筆者也以分數除法的不同表象來解說教師可有的相關專科的教學知識。在教授分數除法時,例如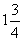 ÷ ÷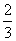 ,部分教師可能只強調計算法則,即除變為乘、跟着顛倒除數的分子和分母,把原式的計算展示如下: ,部分教師可能只強調計算法則,即除變為乘、跟着顛倒除數的分子和分母,把原式的計算展示如下:
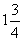 ÷ ÷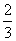 = =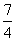 ÷ ÷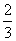 = =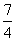 × ×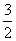 = =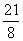 = =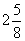
但教師亦可跟據除法的「包含」意義,把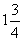 ÷ ÷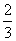 的結果解釋為在 的結果解釋為在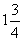 內,有多少個 內,有多少個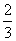 。因此,可以用連減的方法來計算 。因此,可以用連減的方法來計算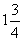 ÷ ÷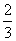 的結果如下: 的結果如下:
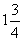 - -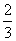 = =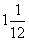 ,而 ,而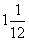 - -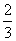 = =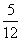 ,因 ,因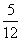 少於 少於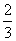 ,所以不夠減 ,所以不夠減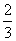 。 。
得出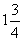 ÷ ÷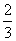 =2… =2…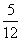 ,即商數是2,而餘數是 ,即商數是2,而餘數是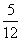 。 。
怎樣可以使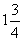 連減 連減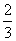 的計算過程更快捷? 的計算過程更快捷?
學生知道同分母的分數加、減只需考慮分子的加、減。因此將被除數和除數化為假分數, 並擴分至同分母,則被除數連減除數的計算過程可簡化如下:
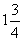 ÷ ÷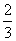 = =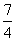 ÷ ÷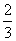 = =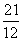 ÷ ÷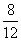 (即在 (即在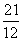 內,有多少個 內,有多少個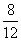 ) )
(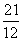 = =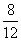 + +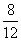 + +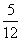 ) )
= 2 … 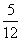 (商數是2,而餘數是 (商數是2,而餘數是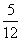 ,即在 ,即在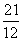 內,有2個 內,有2個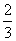 , 餘下有 , 餘下有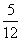 ) )
若只以商數表示結果,則
=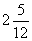 (因餘數 (因餘數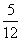 是除數 是除數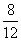 的 的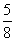 ) )
〔可與21÷8 作比較:21÷8 = 2 … 5 或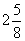 〕 〕
教師亦可以圖像展示以上的分數除法計算。
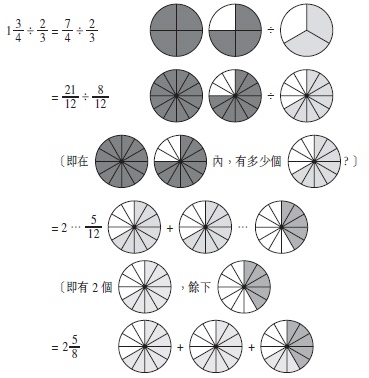
教師可怎樣從以上用連減的策略來計算分數除法演變為傳統的分數除法計算呢?
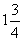 ÷ ÷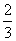 = =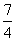 ÷ ÷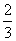 = =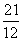 ÷ ÷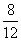 =21÷8= =21÷8=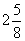
↓
(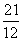 × ×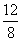 = =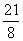 = =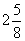 ) )
教師可多用相似上面的具體計算來歸納出分數除法的計算法則,即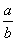 ÷ ÷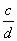 = =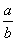 × ×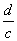 。 。
3. 課程知識( curriculum knowledge) -
課程知識不只是認識某一科目的教學大綱( syllabus/curriculum),還包括熟悉在教授該科目時所需的一系列教材,例如商業市場提供的課本、視聽及資訊科技教材和補充材料;官方提供的有關教學文件和指引等。
為配合有不同需要和興趣的學生,在選取教材時,稱職的教師應充分掌握各式各樣可供選擇的可能性,以達致學生的最佳學習成效。
Lee Shulman 教授還把課程知識細分為:
(a) 橫向課程知識( lateral curriculum knowledge)
充分掌握橫向課程知識的教師能把現時所教的課題與學生同時在其它科目所學的課題相聯繫,並展示相互的關係。就小學數學科而言,數學科教師可把依次在小二和小五教授的課程單位「四個主要方向」和「八個方向」與學生在常識科學習的一些課題作出聯繫,並以這些課題為學習方向的應用示例。
(b) 縱向課程知識( vertical curriculum knowledge)
充分掌握縱向課程知識的教師能就某一科目來說,熟悉學生在前一學習階段所學過的及下一學習階段將會學的知識。同樣地,數學科教師在小五教授課程單位「面積(二)」時,需清楚知道學生在面積這課題上的已有知識及將會怎樣繼續和延伸面積的學習。再以上述有關方向的學習為例,對能力適合的學生,教師可引導學生認識更準確的方法來描述方向,如北、東北偏北、東北、東北偏東等十六個方向,甚至引入初中數學課程的方位角和羅盤法課題。
現時社會對教師的學科知識的要求
現時各地的教育體系都強調「專科專教」,並為師資培訓機構擬訂指引,規範受訓教師的學科知識的最低要求。很可惜,香港在這方面的發展則較落後。
教育學者 Warnock( 1989) 認為「教師的權威主要是基於他們對學科知識的掌握,而普羅大眾對教師能把知識傳授於下一代,表示尊敬」。
諾貝爾文學獎得主蕭伯納( George Bernard Shaw) 就專業人仕的知識就曾說過:
“He who can, does. He who cannot, teaches.”(「有能力的人做他的專業,而無能力的人就去教學。」)
但希臘哲學家亞里士多德( Aristotle) 則說:
“Broadly speaking, what distinguishes the man who knows from the ignorant man is an ability toteach.”(「一般來說,智者與無知的人之分別是智者有施教的能力。」)
筆者希望以上三位大師的名言能為教師起到警惕和鼓勵作用,不時思考自己的學科知識是否足夠應付日常教學的工作,成為一個有專科和專業知識的教師。
編輯後記
《現代小學數學》教材配套備有「 專科教學手冊」,提供學科知識、專科教學知識和課程知識,幫助老師提升專科教學水平。同時,現代教育研究社亦會建立一個交流式的平台 ─「 數學教育專業互動平台」,現代社數學科顧問會透過此平台與老師分享及交流教學心得,並會解答老師有關數學教學上的問題,讓老師得到專業的教學支援。
參考文獻
• Ball, D. L. (1990) The Mathematical Understandings that Prospective
Teachers bring to Teacher Education, The Elementary School Journal,
Volume 90, No. 4, pp. 449-466
• Beishuizen, M. (2001) ‘Different approaches to mastering mental
calculation strategies’ in Anghileri, J. (Ed.) Principles and
Practices in Arithmetic Teaching, pp. 119-130, Buckingham: Open
University Press
• Berliner, D. C. & Rosenshine, B. (1977) ‘The acquisition of knowledge
in the classroom’ in Anderson, R. C. et al. (Eds.) Schooling and
the Acquisition of Knowledge, pp. 375-396, New Jersey, US: Erlbaum
• Dewey, J. (1904/1964) The Relation of Theory to Practice in
Education, National Society for the Scientific Study of Education,
Third Yearbook, Part I, Reprinted in Archambault, R. D. (Ed.)
John Dewey on Education, Selected Writings, Chicago, US:
University of Chicago Press
• Duckworth, E. (1987) Some depths and perplexities of elementary
arithmetic, Journal of Mathematical Behaviour, Volume 6,
pp. 43-94
• Fung, C. I. (1999) Pedagogical Content Knowledge versus Subject
Matter Knowledge: An Illustration in the Primary School Mathematics
Context of Hong Kong, Hong Kong: Unpublished Ph.D. Dissertation,
The University of Hong Kong
• Lampert, M. (1986) Knowing, doing and teaching multiplication, Cognition
and Instruction, Volume 3, No. 4, pp. 305-342
• Ma, Liping (1999) Knowing and Teaching Elementary Mathematics
– Teachers’ Understanding of Fundamental Mathematics in China and
the United States, New Jersey, US: Lawrence Erlbaum Associates,
Inc.
• Martin, G. & Harel, G. (1989) Proof frames of pre-service elementary
teachers, Journal for Research in Mathematics Education,
Volume 20, No. 1, pp. 41-51
• McNamara, D. (1991) Subject Knowledge and its Application: Problems
and possibilities for teacher educators, Journal of Education
for Teaching, Volume 17, No. 2, pp. 113-128
• Post, T. R. (1988) Intermediate teachers’ knowledge of rational
number concepts, Madison, US: National Centre for Research in
Mathematical Sciences Education, University of Wisconsin
• Rosenshine, B. & Stevens, R. S. (1986) ‘Teaching Functions’ in Wittrock,
M. C. (Ed.) Handbook of Research on Teaching 3rd Edition,
pp. 376-391, New York, US: Macmillan
• Rowland, T., Turner, F., Thwaites, A. & Huckstep, P. (2009) Developing
Primary Mathematics Teaching – Reflecting Practice with the Knowledge
Quartet, London: Sage
• Shulman, L. S. (1986) Those Who Understand: Knowledge Growth in
Teaching, Educational Researcher, Volume 15, No. 2, pp. 4-14
• Shulman, L. S. (1987) Knowledge and Teaching: Foundations of the
New Reform, Harvard Educational Review, Volume 57, No. 1,
pp. 1-22
• University of London Institute of Education (1971) An enquiry
into the Education and Training of Teachers in the Area of the Institute
1970/1 – An interim report, Great Britain: King, Thorne & Stace
• van den Heuvel-Panhuizen, M. (2001) ‘Realistic Mathematics Education
in the Netherlands’ in Anghileri, J. (Ed.) Principles and Practices
in Arithmetic Teaching, pp. 49-63, Buckingham: Open University
Press
• Warnock, M. (1989) The authority of the teacher, Westminster
Studies in Education, Volume 12, pp.73-81
• 黃毅英( 2012),《數學教師不怕被學生難倒了:中小學數學教師所需的數學知識》,中國:華中師範大學出版社
|