引言
上文建議教師在課堂教學設計中採用ELPS1 教學模式,並利用數學符號的普遍性和生活情境的特殊性,以培養學生的數學思維。其具體操作就是透過生活情境(E),以鞏固學生已習得的數學知識和建構新的數學概念,並反思數學符號(S)
的意義及其運用的局限。不過,情境化教學設計,要避免數學內涵被淡化,單靠ELPS 模式作為理論基礎並不足夠,筆者認為還需引入其他相關理論,才能更深刻地回答「如何引導學生從現實或非現實情境中,逐漸抽象化而理出相關的數學概念?」這個甚具教學實踐意義的問題。本文從理論角度作思考,集中回應「何謂具現實或非現實情境?」這個問題,至於如何以這些理論思考作指引,以設計非現實情境教學實例,則有待另文分享。
情境化教學設計的理論基礎
從課程發展角度來看,九十年代的「目標為本課程」,提出「現實情景」的教學,強調將生活情境加進數學內容中2。二十一世紀之初的數學課程綱要,亦建議教師多利用日常生活情境,讓學生體驗數學的重要性及其實際的用途(香港課程發展議會,2000;2002)。而大部份前線教師,亦同意利用現實生活情境的好處,如:引發學習動機、提高教學活動的趣味性、培養學生運用數學知識的能力等等。最新版的《現代小學數學》,亦如以往一樣,於教學設計上採用大量的現實生活情境,以回應這方面的要求
( 例見圖一及二)。
| 圖一:乘法 ( 二上B 單元七) |
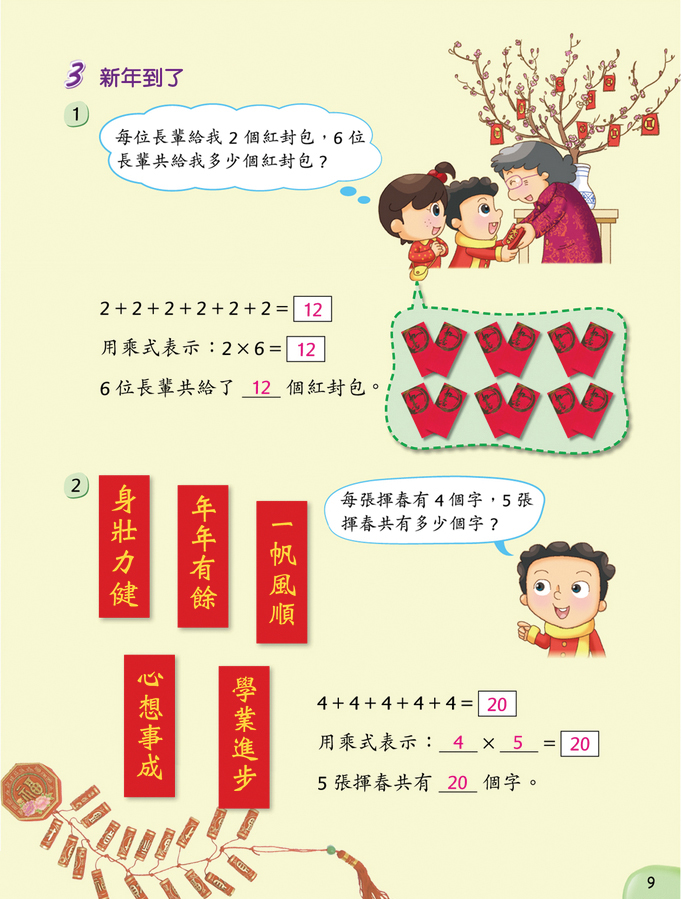 |
| 圖二:圖形的周界 ( 四上B 單元七) |
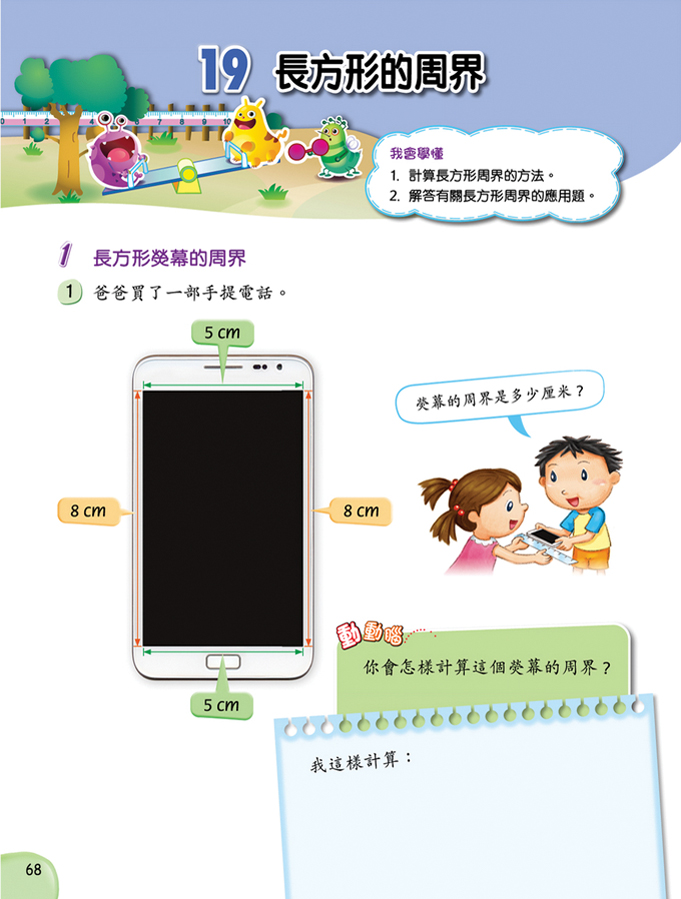 |
但除了現實生活情境之外,教學設計是否可以採用非現實情境?何謂非現實情境?如何選擇合適的非現實情境?⋯⋯筆者會嘗試以數學教育和課程設計兩個理論角度去回答這些問題。
荷蘭的Realistisch Reken Wiskundeonderwijs ( 英譯Realistic
Mathematics Education3),其始創人荷蘭數學家及數學教育家弗蘭登塔爾(Hans Freudenthal),主張數學教學若要保有其人本價值,必須與具情境的世界事例有着密切關係,既要貼切於學生的生活世界,亦要與社會息息相關。數學應被視為一項活動(activity),而非一堆有待灌輸的學習材料。數學教學乃是要提供合適的場景,協助學生進行數學活動,從而「再發明」(re-invent)
數學(Freudenthal,1991;馮振業1999;黃家鳴,2001)。
Realistic Mathematics Education 主張,課堂教學活動都是以具情境的問題
(contextual problem) 為出發點,而這些問題解決之道,往往鼓勵學生採用不同的、非正規的方法去處理,從而讓他們通過「數學化」再創造自己的數學方法。至於何謂具情境的問題,黃家鳴(2001)
的見解非常值得細閱:
“事實上RME (Realistic Mathematics Education)這個英譯亦引起不少誤解,將它等同於‘
real-world’ mathematics education, 等同於以「真實」(authentic) 的處境問題來進行數學教學。但究其荷蘭文本義,動詞(組)‘
zich realiseren’解作想像 (to imagine),因此荷蘭文realistisch其實比英文realistic 有較廣泛的涵義,可以指我們頭腦中所能呈現的、想像的情境,是故在RME
中完全可以採用神仙故事的虛幻世界作情境,只要學習者有能力理解、想像便可以了。” ( 黃家鳴,2001,頁37)。
筆者甚為認同弗蘭登塔爾所主張的具人本價值的普及數學教育( 鄧國俊、黃毅英、霍秉坤、顏明仁、黃家樂,2006),而其具體內涵之一是數學教學活動設計必須是情境化和生活化,但筆者更認同的是,這些情境設計亦應包括兒童日常生活中所觸及和喜愛的具想像非現實經驗,如:益智的童話故事、漫畫、卡通影片、電子遊戲等。至於何謂益智的具想像非現實情境,筆者認為奇雅宏伊勤(Kieran
Egan) 的學養心智理論甚具考參價值。
學養心智理論的啟示
奇雅宏伊勤是加拿大西蒙菲莎大學(Simon Fraser University) 教育學系的教授,其所創立的學養心智
(Educated Mind) 理論與課程設計架構 (Egan, 1988a,1988b,1990,1992,1997,2005,2011)
是非常新穎和具創意的4。其理論架構細緻地探討應如何培養學養心智,並分析幾種不同層面的領悟模式,其理論核心是,學養心智對其外在世界的領悟應包括五個不同層面:肉身層面
(Somatic)、神話層面 (Mythic)、浪漫層面 (Romantic)、哲理層面 (Philosophic) 和吊詭層面 (Ironic)。這些層面的領悟方式都是源自影響我們如何感知世界的各種中介工具,例如語言和文字。這些領悟方式隨着人類演化和文化發展而依次出現;但各種領悟應結合在一起,不能缺一。因此,伊勤
(Egan, 1997) 指出“教育可以理解為個體隨着一定的發展次序,盡量發展各種不同層面的領悟的過程經歷” ( 頁4)。因此,他對教育的看法是源自一種新的文化重演理論
(Recapitulation Theory)。總體而言,兩歲半以下的幼兒主要發展肉身層面領悟,兩歲半至八歲的兒童要主力發展神話層面領悟,八歲至十五歲少年是發展浪漫層面領悟的重要階段,十五歲至廿一歲青年是發展哲理層面領悟的重要階段,而發展吊詭層面的領悟則是成長以後的事。
以下數段文字主要簡介與幼兒及小學教育相關的三個層面:肉身、神話及浪漫層面領悟5,大部份內容主要引自伊勤1997
年的著作《學養心智:認知工具如何塑造我們的領悟》(The Educated Mind: How Cognition Tools
Shape Our Understanding )。
肉身層面的領悟
伊勤指出我們的身體是塑造心智領悟的最基本中介工具,所以他所提倡的可算是一種肉身化 (Embodied)
的哲學。肉身層面的領悟是指“人類因着本身所擁有的身體而對世界所持有的領悟方式”( 頁5)。從次序上來講,肉身式領悟在神話式、浪漫式、哲理式和吊詭式領悟之前,但它不會隨語言發展或其他幾種領悟的出現而有所褪減或被代替。相反,肉身層面的領悟伴隨我們的一生,並與其他層面的領悟一起發展。當然,肉身式領悟也可能因為其他層面的領悟的出現而作出修訂。
神話層面的領悟
相傳為荷馬 (Homer) 所著的兩首古希臘史詩伊利亞特 (Iliad ) 和奧德賽(Odyssey
) 是展示神話式領悟特徵的最佳例子。神話式領悟的特徵之一是二元結構,例子有:男性/ 女性、文化/ 自然、理性/ 感性、自我/ 他人、人物/
背景以及陰/ 陽等。神話式領悟的另一特徵是幻想。“世界不同地方的兒童幾乎都會對幻想故事中那些稀奇古怪的事物而感到雀躍不已,例如是穿上衣服、會說話的兔子、小熊或其他動物”(
頁44)。其他的特徵還包括抽象思維、比喻、韻律、情節和映像。伊勤認為,這些特徵是口語發展的必然結果,這對於世界上不同地方、歷史上不同階段的口語社會,或者是世界各地兒童在學習運用語言的過程中,都是必然出現的結果。
浪漫層面的領悟
伊勤認為浪漫層面的領悟是由讀寫能力發展所建立的一種獨特的領悟方式。希羅多德 (Herodotus)
的《歷史》(Histories ) 是浪漫式領悟的一個早期和相當清晰的體現。這部著作寫於公元前600 年,這時文字書寫開始融入古希臘的社會生活當中。“《歷史》這部著作就像古代的健力士紀錄大全,當中充滿了歌頌勇敢和高尚品德的故事,關於域外和奇特見聞的描述,令人讚歎的成就,以及對碩大無朋、奇形怪狀的建築物所發出的讚美句語。如果沒有文字書寫的話,這個層面的領悟便不容易展示出來”(
頁83)。浪漫層面的領悟不單見於古希臘或其他古文明( 如中國),也在某程度上出現在人們撰寫和閱讀這些文字時,或聆聽別人作演講和表演時所作出的思考。以下是浪漫式領悟的某些特徵:(一)現實中的極限、極致的經驗、生活中的背景;(二)在現實當中作出超越;(三)人性化的知識;(四)浪漫形式的理性。總括而言,浪漫層面的領悟的主要特徵是神話和理性的
結合。
簡而言之, 要判斷何謂益智的具想像非現實情境,以學養心智理論角來看,就是能啟發小學階段兒童的神話和浪漫層面領悟而又具文化內涵養份的情境和生活經驗。此外,奇雅宏伊勤的學養心智理論亦非常關注理念實踐上的各種細節,從而推動以兒童領悟學習為中心和激發其想像力的教學設計,但由於篇幅所限,有關具想像非現實情境的教學設計實例分享,只可留待下回分解6。
總結
本文從理論角度出發,集中回應「何謂具現實或非現實情境?」這個問題。弗蘭登塔爾主張數學教學若要保有其人本價值,數學應被視為一項活動(activity),而非一堆有待灌輸的學習材料。數學教學乃是要提供合適的場景,協助學生進行數學活動,從而「再發明」(re-invent)
數學。其具體內涵之一是數學教學活動設計必須是情境化,而情境設計亦應包括兒童日常生活中所觸及和喜愛的具想像非現實經驗。奇雅宏伊勤的學養心智理論與弗蘭登塔爾的數學教育主張,甚具理論上的共通性。兩者的教育思想都以人為本,強調普及教育的重要,而且非常關注理念實踐上的各種細節,從而推動以兒童理解/
領悟為中心和激發其想像力的教學設計。
參考文獻
香港課程發展議會(2000),《數學教育學習領域:數學課程指引 (小一至小六) 》,香港:政府印務局。
香港課程發展議會(2002),《數學教育:學習領域課程指引(小一至中三)》,香港:香港印務局。
馮振業(1999),〈數學化教學:從夢想到現實〉,載黃毅英、黃家鳴( 編),《基礎數學教育的優化研討會論文集》(
頁4 - 46),香港:香港中文大學教育學院課程與教學學系。
馮振業(2004),〈數學化教學:理論、實踐與前瞻〉,載鄧幹明、黃家樂、李文生、莫雅慈( 編),《香港數學教育會議
─ 2004 論文集》( 頁78-88),香港:香港大學教育學院。
馮振業(2007),〈略述數學化教學的九大關注項目〉,載梁志強、黎敏兒、潘建強、梁景信( 編),《香港數學教育會議2007
論文集》( 頁152-164),香港:香港數學教育學會。
黃家鳴(1997),〈生活情境中的數學與學校的數學學習〉,《基礎教育學報》7 卷12 期,161-167。
黃家鳴(1998),〈數學文字題及課業的處境應該有多真實?〉,《數學教育》7 期,44-54。
黃家鳴(2001),〈現實情境作為數學學習的起點:荷蘭經驗〉,《數學教育》11 期,34-46。
鄧國俊(2005),〈初中有向數的教與學:隱喻理論與學養心智理論的啟思〉,載黃毅英( 編),《蕭文強教授榮休文集:迎接新世紀重新檢視香港數學教育》(
頁126-140),香港:香港數學教育學會。
鄧國俊、黃毅英、霍秉坤、顏明仁、黃家樂(2006),《香港近半世紀漫漫「小學數教路」:現代化、本土化、普及化、規範化與專業化》,香港:香港數學教育學會。
鄧國俊、鍾永康(2003),〈數學史與數學課程改革:學養心智理論的啟思〉,載鄧幹明及曾倫尊( 編),《學會學習:數學課程改革評析》(
頁92-109),香港:香港數學教育學會。
Egan, K. (1988a). Primary understanding: Education
in early childhood . New York and London: Routledge.
Egan, K. (1988b). Teaching as story telling :
An alternative approach to teaching and the curriculum. London:
Routedge.
Egan, K. (1990). Romantic understanding: The development
of rationality and imagination, Ages 8-15 . New York and London:
Routledge.
Egan, K. (1992). Imagination in teaching and learning:
The middle school years. Chicago: The University of Chicago Press.
Egan, K. (1997). The educated mind: How cognitive
tools shape our understanding. Chicago: The University of Chicago
Press.
Egan, K. (2005). An imaginative approach to teaching
. San Francisco: Jossey-Bass Publishers.
Egan, K. (2011). Learning in depth: A simple innovation
that can transform schooling. Chicago: The University of Chicago
Press.
Freudenthal, H. (1991). Revisiting mathematics
education: China lectures. Dordrecht: Kluwer Academic Publishers.
Liebeck, P. (1984). How children learn mathematics:
A guide for parents and teachers. Harmondsworth: Penguin.
1 E-Experience 經驗實作,L-Language 數學語言,P-Picture 圖像思維,S-Symbol 數學符號。
2 更早可追溯至七十年代普及教育推行之初 ( 鄧國俊、黃毅英、霍秉坤、顏明仁、黃家樂,2006)。
3 本文刻意不提中譯「現實主義數學教育」,原因是這個中文譯名或許有點誤導,黃家鳴(2001) 在其〈現實情境作為數學學習的起點:荷蘭經驗〉一文,亦因此原因而表明只是暫且採用。
4 讀者如有興趣作初步了解,可登入The Imaginative Education Research Group (IERG) 網址:http://ierg.net/。
5 讀者如對有興趣更深入了解,可參閱鄧國俊 (2005) 及鄧國俊、鍾永康 (2003),或找原著細閱。
6 讀者如對其他科目實例感興趣,可登入The Imaginative Education Research Group (IERG) 網址:http://ierg.net/。 |