引言
上文提到數學雖然具嚴謹性和抽象性，但生活化和情境化就是數學思維的基石，集與邏輯亦是從這些基石而來。故在數學教學中引入具現實或非現實情境的生活化、遊戲化、故事化等教學設計，是值得大力提倡的。當然，「如何引導學生從具現實或非現實情境中，逐漸抽象化而理出相關的數學概念？」及「如何用嚴謹的數學方法得出結論？」等問題亦要小心回應，以免掉入數學的特質被淡化而至課堂教學形同「兒戲」這陷阱。本文先以ELPS
理論為基礎，然後探討數學符號的普遍性和生活情境的特殊性，最後以現代教育研究社於2014 年出版的《現代小學數學》教科書內的基本除法及分數除法的教學設計實例，探討如何透過生活情境，反思數學符號的意義及其運用的局限，以培養學生的數學思維。
ELPS教學模式
「如何引導學生從具現實或非現實情境中，逐漸抽象化而理出相關的數學概念？」，英國數學教育家Pamela
Liebeck 所建議的方法是ELPS1 教學模式 (Leibeck, 1984)，相信不少香港教師亦接觸過有關理論，甚至嘗試應用實踐。現以小二基本除法為例，為一些未接觸過此理論的讀者作簡單說明。
分物遊戲是基本除法教學的引入點，《現代小學數學》二下B 單元六採用了多種具現實的生活例子，如分貝殼、分糖果等
( 例見圖一)。學生在進行課堂活動時，首先是以教師所提供的實物或教具，去感覺和體驗分物過程和結果(E)，教師亦應鼓勵同學在小組活動過程中，多以數學語言作解說和討論(L)、並多用圖像以輔助思考和加強溝通(P)，然後以連減法的數學算式作記錄(S)2。透過不同的生活實例，學生在這單元所習得有關均分、包含、無餘數和有餘數的分物技能和知識，將成為其往後學習單元七的除式、乘除關係和基本除法的基礎。長遠而言，這些技能和知識更是其日後於高小學好分數除法的重要基石。
圖一：分糖果( 包含意義的分物——無餘數)
數學符號的普遍性和生活情境的特殊性
ELPS 教學模式由於具理論價值和實踐驗證，故能得到教師廣泛接納和採用(Haylock& Cockburn,
2008)。但據筆者個人觀察，無論是學者或是前線教師，多從經驗實作(E) 開始，到數學符號(S) 作結。較少從具普遍性的抽象數學符號(S)，去回看各種生活情境(E)的特殊性，並反思數學符號(S)
的意義及其運用的局限。現先以下面兩個例子說明何謂生活情境的特殊性和數學符號的普遍性3。下一節則會以教學設計實例，來探討如何透過生活情境，反思數學符號的意義及其運用的局限，以培養學生的數學思維。
正如上一期文章( 一) 所提，人類與生俱來有一種數字感 (Number Sense)，讓我們能夠以直觀方式明白自然數及其基本的運算。我們不能夠避免看到物件的顏色，亦很快便學會說出物件的顏色⋯⋯同樣，數量的概念、數數(Counting
Number) 及簡單加減運算亦很早便成為我們生活中的一部份，並作廣泛而普遍應用。但有些時候，因為某個生活情境的特殊性，使我們在運用一些非常簡單的數量概念、數數或加減運算時遇上意想不到的困難。
第一個簡單而深刻的例子，就是有關美國世貿大廈於2001 年9 月11 日的事件中，究竟是受到一次襲擊還是兩次襲擊所引起的法律訴訟。擁有這兩座大樓的房地產商認為是兩次，而保險公司則認為只是一次4。如果陪審團裁定為一次襲擊，有關房地產商將得到30
億美元賠償；如果裁定為兩次，整個賠償額將高達70 億美元。訴訟事件的特殊意義不單只在金錢賠償的多寡，更成為日後相關保險賠償訴訟裁決的依據5。另一個例子是太陽系中行星的數目。2006
年，在捷克布拉格舉行的第26 屆國際天文學聯會通過決議，將冥王星降級成矮行星，使太陽系的行星數目由九減為八。以上兩個例子，使我們深深體會到簡單如數數技巧，有時因為情境的特殊性而令我們應用時出現困難，但亦促使我們對數學思維及其運用有更深刻的體會和反思。
透過生活情境以培養數學思維：教學設計實例
以上的觀察和反思， 對前線教師的課堂教學有何啟示？現試以分數除法的教學設計，探討如何透過生活情境(E)，反思數學符號(S)
的意義及其運用的局限，以鞏固學生已習得的數學知識和建構新的數學概念，進而有效地培養數學思維。
分數除法教學的引入，《現代小學數學》五下A 單元四同樣採用了多種具現實的生活例子，如分蛋撻、分砂糖等（例見圖二及三）。學生在進行課堂活動時，會以教師所提供的教具(
如手工紙)，去感覺和體驗分物過程和結果(E)，同樣地，教師亦應鼓勵同學在小組活動過程中，多以數學語言作解說和討論(L)、並多用圖像以輔助思考和加強溝通(P)，然後透個數個實例，以歸納出如何利用倒數來作分數除法這個具普遍應用價值的計算方法(S)。
圖二：分蛋撻( 整數除以分數)
圖三：分砂糖( 分數除以分數)
教師透過適當及適量的堂課及功課練習，使學生對利用倒數來作分數除法的知識和技巧有充分的掌握後，便可引入更高層次的數學思維作為學習目標。圖四及圖五所設置的三個不同的情境，就是用來鞏固學生已習得的具普遍性的分數除法，和建構分數除以分數(
有餘數) 這個新的數學知識，並反思數學符號的意義及其運用的局限，以培養學生的數學思維。
圖四的分氣球及分繩子情境並排而列，用意是幫助學生去觀察這兩個生活情境的特殊性，從而明白在分數世界中，簡單如整數除以整數，在應用分數除法的概念和技巧時(S)，亦要視乎每個情境的特殊性(E)
而作出決定。圖五的絲帶分段情境，學生如果只懂機械化地背誦公式和演算程序(S)，就算他能準確無誤地算出正確答案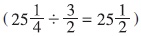 ，亦只能算是完成解難活動的一半，這正好帶出利用倒數來作分數除法(S)
的局限。要為這絲帶分段情境(E) 找出正確答案，尤其是餘數(1/4 米= 25 厘米)，就要有充足的基礎知識及運算概念，同時亦要有嚴謹的推理能力和態度，才能得出結果。此外，圖五「數學小檔案」中所介紹的疊除法計算方法，除可用以鞏固小二及小四所習得的數學知識
( 圖一及圖六)，更可透過分析和比較這兩種運算方法6，使學生反思數學符號的意義及其運用的局限，以培養學生的數學思維。
圖四：具對比性的情境
圖五：分數除以分數( 有餘數)
圖六：不同方法計算兩位數除三位數
總結
首先，「如何引導學生從具現實或非現實情境中，逐漸抽象化而理出相關的數學概念？」，本文的結論是，ELPS
教學模式實在值得教師嘗試採用。至於何謂具現實或非現實情境，筆者會於日後另文分享。其次，「如何利用數學符號的普遍性和生活情境的特殊性，以培養學生的數學思維？」，本文的建議是在課堂教學設計中，透過生活情境(E)，以鞏固學生已習得的數學知識和建構新的數學概念，並反思數學符號(S)
的意義及其運用的局限。此外，要有效地培養數學思維，學習過程中必須使學生明白，如只懂機械化地背誦公式和演算程序，就算能準確無誤地算出正確答案，亦未必能將難題解決。要習得良好的解難能力，先要有充足的基礎知識及運算概念，同時亦要有嚴謹的推理能力和態度。總而言之，我們在設計情境化教學時，如能注意以上各要點，便不會掉入數學的特質被淡化而至課堂教學形同「兒戲」這陷阱。
參考文獻
Liebeck, P. (1984). How children learn mathematics:
A guide for parents and teachers.Harmondsworth: Penguin.
Haylock, D., & Cockburn, A. (2008). Understanding
mathematics for young children : A guide for foundation stage and
lower primary teachers (Revised and expanded edition). Los Angeles;
London : SAGE.
1 E-Experience 經驗實作，L-Language 數學語言，P-Picture 圖像思維，S-Symbol 數學符號
2 建議學習初期不要過份強調精準的數學語言和嚴謹統一的數學算式。
3 這兩個例子未必適合作小學教學用途。
4 房地產商的依據是，兩次撞擊先後相隔15 分鐘，但保險公司認為，劫機行動是統一策劃的。
5 2013 年2 月，英國商業法庭(English Commercial Court) 裁定為兩次，整個訴訟到裁決耗時約十年。
6 除利用倒數和疊除法這兩種方法外，通分母亦是一個利用符號運算(S) 去求答案的方法，非符號運算的方法則包括實作(E)、作圖(P)和利用計數機等方法。教師可按學生能力去引導學生學習部份或全部的方法，並作比較分析。
|