前言
小學數學課程中,「數」範疇所佔的比重最大,以課程文件所建議的教學節數計算,小一至 小四的課程內容中,屬於「數」範疇的約佔55%
之多,而在小五、小六,比重也達到43% 。可見「數」範疇是整個數學課程的最主要部分,而構成這一主要部分的,首先是整數、分數、小數和百分數的四則運算,其次就是與這些運算相關的應用題了(當然,也有其他的內容)。因此,應用題的學與教向來都受到相當的重視。
應用題的學習難點
相比計算題,解應用題會較難一些,因為應用題並不像算式那樣清楚表明要計算甚麼,學習者需要理解題意,自行判斷該進行甚麼運算,寫出算式,才計算答案。但正如論者所指出的那樣,同一運算的應用題可以有多種題型,比如加法應用題可以有「合併」、「增添」、「比較」、「原有」等題型,減法應用題可以有「餘下」、「尚欠」、「比較」、「找回」等題型。對學習者而言,他們不是一開始就知道這林林總總的題型,而是在學習過程中逐一認識和掌握的。當題型知識足夠且組織得好時,他們就能對解題所需的運算作出正確判斷;反之,當題型知識不全面或有混淆時,他們就常常作出錯誤判斷,於是學習上便出現了難點,即使低年級也不例外。舉例來說,在1
下「100 以內的加法」有這樣一道例題:
玩具結他有19 個,玩具琴比玩具結他多11
個,玩具琴有多少個?
這問題看似簡單,計算19 + 11,便可找出答案30。但對小一學生來說,這可以是一道令他產生混淆的應用題。因為在此之前,加法應用題只有「共有」一種題型(如:爸爸有橙8
個,媽媽有橙4 個,爸爸媽媽共有橙多少個?),而減法應用題則有「還有」(如:魚缸有魚11 條,取走了6 條,還有魚多少條?) 和「比⋯多多少」(如:小康有12
輛玩具車,小光有8 輛玩具車,小康的玩具車比小光的多多少輛?)兩種題型,小一學生遇到上面的問題,在讀到「玩具琴比玩具結他多11
個」時,自然聯想到「比⋯多多少」這一減法題型,直覺認為要計算「19 – 11」。但當老師告知應計算「19 + 11」,他們就可能大惑不解:題目沒問「共有」,為甚麼要計加?題目有「比⋯多」,為甚麼不計減?要解決學生心中的疑惑,教師固然可以利用簡單數字或圖示來說明為甚麼加法才是正確運算,但更徹底的做法似乎是把兩種易混淆的題型加以對照:
小康有12 輛玩具車,小光有8
輛玩具車,小康的玩具車比小光的多多少輛?
玩具結他有19 個,玩具琴比玩具結他多11 個,玩具琴有多少個?
讓同學思考和討論,找出它們的分別。當同學明白這是兩種不同的題型時,他們就容易接受解題運算也會不同。
1
下的另一個難點,就是連加問題,如:
渡輪下層有乘客28 人,上層乘客比下層多33 人,渡輪的上、下層共有乘客多少人?
這是「共有」的題型,同樣也給出兩個數,但要進行「28 + 33 + 28」的三數連加,與之前的「共有」題型大不相同。教師多知道這是一個難點,而且會採用一些方法,例如表列法,來幫助學生寫出正確算式:
| 下層 |
28 |
| 上層 |
28 + 33 |
| 上、下層共有 |
28 + 33 + 28 |
但最理想的是同學也能通過比較對照,找出這種「共有」題型和一般的「共有」題型有甚麼分別,從而有助他們辨別出連加計算的應用題,然後運用老師所教的方法,如表列法,把正確算式寫出。
到了2 上,又有一個難點出現。試看以下兩個比較應用題:
1. 小娟有45
個郵票,弟弟的郵票比她多28 個,弟弟有多少個郵票?
2. 小娟有45
個郵票,比弟弟的多28 個,弟弟有多少個郵票?
它們十分相似,除了首、尾相同外,中間都有「比⋯多若干個」的用語,但其實它們是不相同的:第1 題要計算「45
+ 28」,第2 題則要計算「45 – 28」。即是說,有「比⋯多」用語的應用題不一定都是加法題,它們也可以是減法題,這點小二學生最感困惑。要幫助學生正確寫出算式,教師可用表列法,列出誰多誰少來決定應該計加還是計減,如:
1.
2.
此外,如何幫助學生區分這兩種十分相似但運算完全不同的應用題,也是十分重要的,這點下文再作討論。
從小三開始,學生開始學習多步的混合計算,應用題也相應變得複雜。儘管題型看似和以往分別不大,但題目文字通常較長,給出的數據較多,描述的關係也較複雜,部分學生未能應付得到,於是便成為學習上的新難點。以下就是一個典型的例子:
樂園餐廳前天的收入是4354 元,昨天的收入是3215 元。今天的收入比昨天的多397 元,
今天的收入比前天的少幾元?
要幫助學生應付這冗長的文字題,把問題細分是一個常用的方法,如把問題改為:
樂園餐廳前天的收入是4354 元,昨天的收入是3215 元。今天的收入比昨天的多397 元。
(a) 今天的收入是多少元?
(b) 今天的收入比前天的少幾元?
也可以通過填表方式將問題細分:
填一填、算一算:
樂園餐廳前天的收入是4354 元,昨天的收入是3215 元。今天的收入比昨天的多397 元。
| 前天的收入 |
|
| 昨天的收入 |
|
| 今天的收入 |
|
| 今天的收入比前天的少 |
|
隨着題目變得複雜,題目的形式也多了變化,包括:
(1) 部分資料在圖中,不在題目內,學生要細看附圖才能找到足夠的資料。
(2) 資料隱藏在情境中,如:
爸爸和4 位同事一起到酒樓享用了一個晚飯套餐,費用由大家分擔,每人需付285 元。
這個晚飯套餐售多少元?
題目沒有說明費用由多少人分擔,但它的開首部份暗示了總人數是5。
(3) 題目包括了多餘的資料,同學要避免錯誤地選用它於計算中。
以上這些也可能成為學習上的難點。
另外,分部的應用題常會包含一些延伸問題讓學生解答,如:
每碗雲吞麫需要4 粒雲吞,現有23 粒雲吞。
(a) 共可製成雲吞麫多少碗?餘下雲吞多少粒?
(b) 要把餘下的雲吞也製成一碗雲吞麫,還欠雲吞多少粒?
把131 份試卷,平均分放在4 個公文袋內。
(a) 每個公文袋有試卷多少份?餘下多少份?
(b) 把餘下的試卷也放入其中一個公文袋內,這個公文袋內有試卷多少份?
兩題的(b) 部都是延伸問題,但它們不像(a) 部那樣只需計算除法便可,而是要根據題意和(a) 部得到結果,進行另外的計算,以解決特定的問題。於是,這亦可以成為學習上的難點。
總括來說,應用題的學習難點主要是基於以下四個原因:
(1) 多樣的題型,
(2) 複雜的文字,
(3) 多變的題目形式,和
(4) 非常規的延伸問題。
應用題的教學策略
根據以上對應用題學習難點的探討,我們可相應地提出一些應用題的教學策略。
1. 比較對照容易混淆的題型讓學生清楚它們的區別此點上文已有提及,茲不贅。
2. 強化應用題的題型與運算間的聯系
上面見到,特定的題型是和特定的運算相關的,要有效解應用題,學生就必需熟習各類題型與其相應運算間的聯繫,為此,教師可以通過一些活動,如「續寫算式」和「自擬問題」等來強化學生這種聯繫。
續寫算式
例如,教師給出「每瓶牛奶糖有150 粒,買了3 瓶,
。」,着學生續寫算式。學生觀察到題型是「每瓶有⋯粒,有⋯瓶」,這是典型的乘法題型,不需問句也知道可以計算乘法找出共有牛奶糖多少粒,於是在空位上填上「共有牛奶糖
150 | 3 粒」。
又例如,教師給出「10 張 DVD 售 650 元, 。」學生認識到這是「一組相同的物件售⋯元」的除法題型,不需問句也知道可計算除法找出每件物件售多少元,於是在空位上填上「每張
DVD 售 650 ÷ 10 元」。
經過這類活動,學生強化了題型和相應運算間的聯繫後,當遇上較複雜的問題,就可以更有效地寫出算式。例如:
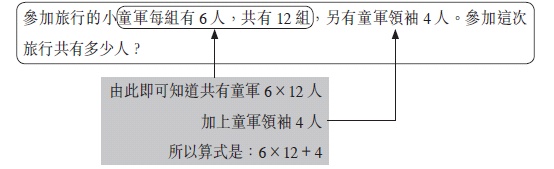 |
自擬問題
例如,教師給出一個問題情境,着學生擬出不同類型的應用題:
以下是一些超市物品的售價:
乳酪 每杯
$ 6.00
朱古力條 每袋 $14.00
提子汁 每罐
$ 9.00
餅乾 每盒
$23.00 |
(1) 自擬一題加減混合計算的應用題。
(2) 自擬一題乘加混合計算的應用題。
(3) ⋯
學生自擬過某一類型問題後,以後解題時再碰上同類問題,就會更有信心確信這是哪一類問題,應該怎樣做了。
這裏也要留意到,教師提供了問題情境後,學生只需擬出問句便夠〔如第(2) 題的問句可以是「買兩杯乳酪和一罐提子汁共需付多少元?」〕,因此不需要書寫太多文字。低年級學生更可以口述問題,避免因書寫文字而耗費太多時間。
3. 教導學生繪畫適當圖形以助解題
所以教師應教導學生如何按題意畫出圖示,否則當遇到較複雜的問題時,他們就不可能畫出適當的圖示以助解題。
四則應用題的基本圖示不多,主要有以下數種:
(1) 整體和部分問題
(2) 比較問題(多、少、相差、貴、便宜、找回)
(3) 乘除應用題
由於種類不多,內容簡單,要學生繪畫這些圖示,應不會有特別困難。問題是在甚麼時候要學生畫?如果在他們開始學習某類應用題的時候也同時要求畫出圖示,相信學習效果不會太好。比如:
一盒月餅有4 個,6 盒月餅有多少個?
學生根據乘法口訣「四六二十四」,很快就知道答案是24。若要學生先繪出以下圖示:
才去計算答案,由於繪圖甚花時間但對解題無甚幫助,學生的學習意欲就會頗低,不大願意認真把圖畫好。
因此,學生繪畫活動似宜結合較複雜的問題(不一定是應用題)進行,讓他們看到繪圖真能幫助解題,便會增加他們的學習誘因。例如:
在這學習活動中,學生固然學習了解答減法的逆向問題,但同時也學習了繪畫「整體和部分關係的圖示」。
另外,「比較的圖示」可以結合連加法來學習,「乘、除的圖示」也可結合乘加、除加、乘除等混算來學習。總之,圖示的繪畫若能把複雜的問題簡化,能有助問題的解決,就可以突顯它的用處,因而使學生樂於學習。
4. 教導學生適當地轉化題目內容
(1) 理順比較關係
上文提到以下的比較應用題:
小娟有45 個郵票,比弟弟的多28
個,弟弟有多少個郵票?
認為這問題容易引起混淆,因題目中有「比⋯多」的用語,卻要計算減法「45 – 28」才可得到答案。
為甚麼容易引起混淆呢?細看此題,我們會發現題目的中間部分和結尾問句存在不一致的情況:
問句是問弟弟的郵票數目,
中間部分是描述小娟的情況〔
(小娟的郵票)比弟弟的多 28個〕而不是弟弟的情況,
若直接用中間部分來進行計算,即是用小娟的情況來計算弟弟的郵票數目,答案當然不正確。
不過,若把中間部分小娟和弟弟的比較關係倒轉表述,即將問題轉化為:
小娟有45 個郵票,弟弟的郵票比小娟的少28
個,弟弟有多少個郵票?
我們就可用弟弟的情況來計算弟弟的郵票數目,從而得出正確答案45 – 28 了。
由此見到:
以上提供的判斷和轉化方法(「主語」是否出現兩次?若是,便把比較關係倒轉表述)為教師在幫助學生應對易生混淆的比較應用題時提供了多一種處理方法上的選擇。
(2) 把題目簡化
看看以下例子:
裝飾每個禮物盒需用彩繩3 束,每束15 條。
現有彩繩270 條,最多可裝飾禮物盒多少個? |
這題給出3 個數據,通常會視作為兩步運算的應用題。注意到第一個句子是典型的乘法題型,如果改以乘式把它表述出來,題目就會轉化為:
裝飾每個禮物盒需用彩繩15 × 3 條。
現有彩繩270 條,最多可裝飾禮物盒多少個? |
簡化成類似一步的除法應用題,使同學較易看到算式是270 ÷ (15 × 3)。同樣,以下問題也可作類似的簡化:
令學生容易明白算式是112 ÷ (48 ÷ 6)。
(3) 增補內容,使前後連接不暢順的題目讀起來較為暢順
看看以下例子:
此題前後兩半的連接並不暢順,讀題過程中,令人有種驟然轉向的感覺。然而,當作了簡單的增補後:
以上種種題目內容的轉化技巧,教師如能適當地介紹給學生,當有助他們理解和應對較複雜的應用題。
|