電子學習需要學生經常運用電子資源發展二十一世紀能力。二十一世紀能力包括探究能力、批判思考能力、合作和溝通等能力。學校教育需要在各學科課程,透過不同課題如「分數相乘」的電子學習,提供學生探究及反思的機會,於無縫學習環境的學習過程同時發展學科知識及二十一世紀能力。要達到這個教育目標,教師既需要掌握教學課題的科本核心意義及教學方法,亦需要懂得發展二十一世紀能力的教學技巧。教師因此需要合適的專業發展提升個人的教學能力,迎接電子學習為學校教育帶來的挑戰。
要有效提升教師在數碼教室推動學生發展二十一世紀能力,相關的電子學習教師發展活動需要培養教師善用教學設計為學生創建探究學習環境的能力,然後整合能力於日常教學工作,讓教師有機會反覆地實踐和改進教學設計。教師透過學生學習成果及實踐社群的討論及反思,漸進地改進教學設計,從而不斷發展個人在數碼教室推行以學習者為中心的教學能力
( 見圖1)。當中的教師實踐社群可由任教相同學科課題的教師所組成,並由教師培訓專業人員或學校資深科任教師組織成員反思及改良教學設計
(Kong & Song,2013; Wenger, 1998)。
上述的專業發展架構需要三個元素落實。( 一) 教師需要懂得按所選課題特性挑選適合的數碼資源作探究學習用途:有關的數碼資源需要在內容及設計上蘊含並反映該課題的核心意義,讓學生能夠通過所選的數碼資源自行探究得出該課題的重要概念。(
二)教師充分認識所選課題的科本核心意義:教師通過個人自習或實踐社群討論,深化自己的科本學養及對所選課題的認識,建立基礎構思有效的教學設計。(
三) 教師能夠設計善用所選數碼資源的教學:教師的設計需要配合所選課題教學特點及所選數碼資源教學潛能的教學方法,引導學生有效地運用數碼資源探究該課題的核心意義。
分數相乘是基礎教育數學課程的核心課題。下文以「分數相乘」這數學課題為例,討論一個有關運用數碼資源促進分數相乘教學的電子學習教師發展活動,闡述數學教師如何在教學設計上加入電子學習元素,透過學科知識教學發展學生的二十一世紀能力。
學生學習與分數相關的課題時需要掌握基本分數概念,並了解關鍵的分數屬性,從而發展有理數知識。常見分數有五種數學觀點:
部份─ 整體、度量、比、操作和商(Lamon, 2001; Prediger, 2008)。因為部份─整體觀是最自然的學習觀點,所以當前的數學教育最常選用這觀點作為分數教學的切入點(Lamon,
2001)。不過研究顯示部份 整體觀不利學生進一步學習有理數的數學系統,並不適合作為分數教學的主要的教學重點;反而分數的度量觀點較有利學生發展有理數的知識
(Lamon, 2001)。
分數相乘有兩個基本意義:( 一) 分數乘整數作為重覆相加這個分數─這個操作具擴展被乘數大小的含意;(
二) 一個真分數的被乘數乘以一個單位分數─此意義在於進一步切割被乘數的分數部份,然後從中取某部份的一個操作,這個操作具收縮被乘數大小的含意
(Isiksal & Cakiroglu, 2011; Izsák, 2008)。在學習分數相乘的課題時,學生還要理解分數的操作觀點,明白分數相乘是一項複合運算操作,其中包括一個收縮操作和一個擴展操作。
電腦支援的認知工具可支援、引導及促進學生在認知過程中對學習課題的認識和理解 (Rittle-Johnson
& Koedinger, 2005;Roschelle, Rafanan, Bhanot, Estrella, Penuel,Nussbaum,
& Claro, 2010)。圖2 顯示了一個源於「分數相乘」全貌及本質分析的認知工具的介面設計。這個認知工具的模擬圖像模型蘊含了分數相乘的重要概念和複合操作原理,並包含特定的解說如操作的收縮及擴展的情況和條件、怎樣判斷分數相乘結果和原來分數的大小比較的內涵本意等。
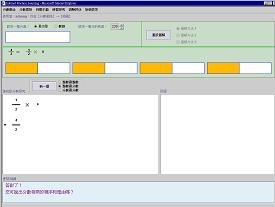 |
圖2a:認知工具演繹「分數相乘」第一個重要意義的模擬圖像模型表示─
分數乘整數的重複相加分數。 |
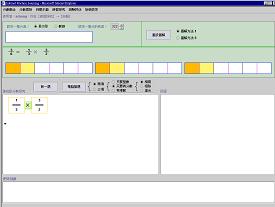 |
圖2b:認知工具演繹「分數相乘」第二個重要意義的模擬圖像模型表示─
一個真分數的被乘數乘以一個單位分數( 即進一步切割被乘數的分數部份,然後從中取某部份的一個操作)。 |
教師可在相關的數學課堂裏,運用上述認知工具支援、引導及促進學生在認知過程中對「分數相乘」這課題的認識和理解;並設計配合學生日常生活情境的「分數相乘」探究題目,讓學生以小組形式與學伴一起運用認知工具探索「分數相乘」的重要概念和運算操作。教師同時可鼓勵學生多嘗試選用認知工具所提供的不同圖解方法,從多角度了解分數相乘的意義;並鼓勵學生課後嘗試認知工具所提供的練習或測驗題目,然後定期查看學生完成有關練習或測驗題目的情況,從中了解學生的學習進度及學習困難。這樣的教學設計可讓學生通過認知工具的題庫參與探究分數相乘概念和操作的問題、通過認知工具的運算介面探索分數相乘的運算方法、通過認知工具的互動圖解解釋探究分數相乘的結果、通過認知工具的即時回饋評估探究分數相乘的結果,及通過認知工具的額外練習延伸分數相乘的課題探究。
這個分數相乘教學方法先從部份─整體觀點切入,然後以度量觀點深化學生對分數意義的理解,再以分數操作觀教授學生相關的運算技巧,讓學生從多觀點多角度了解分數的意義,並於三方面應用二十一世紀能力:(
一) 歸納出分數相乘的運算方法、( 二) 初步建立對常見分數操作觀的認識和理解、( 三)比較在分數相乘過程中的收縮操作和擴展操作如何影響乘數結果的數值大小的能力,然後反思一個常見的誤解:分數相乘結果的數值一定比原來的被乘數分數的數值較細。
上述的例子闡明教師需要懂得按所選課題特性挑選適合的數碼資源作探究學習用途,充分認識所選課題的科本核心意義,並設計善用所選數碼資源的教學設計,讓學生在日常教室學習過程裡有意義地同時發展學科知識及二十一世紀能力。
參考資料:
Isiksal, M., & Cakiroglu, E. (2011). The nature
of prospective mathematics teachers’pedagogical content knowledge:
The case of multiplication of fractions. Journal of Mathematics
Teacher Education, 14 (3), 213-230.
Izsák, A. (2008). Mathematical knowledge for teaching
fraction multiplication. Cognition and Instruction, 26 (1),
95-143.
Kong, S. C., & Song, Y. (2013). A principlebased
pedagogical design framework for developing constructivist learning
in a seamless learning environment: A teacher development model for
learning and teaching in digital classrooms. British Journal of
Educational Technology, 44 (6), E209-212.
Lamon, S. J. (2001). Presenting andrepresenting from
fractions to rational numbers. In A. A. Cuoco, (Ed.), The roles
of representation in school mathematics (pp. 146-165). Reston,
VA: NCTM.
Prediger, S. (2008). The relevance of didactic categories
for analysing obstacles in conceptual change: Revisiting the case
of multiplication of fractions. Learning and Instruction, 18
(1), 3-17.
Rittle-Johnson, B., & Koedinger, K. R. (2005).
Designing knowledge scaffolds to support mathematical problem solving.
Cognition and Instruction, 23 (3), 313-349.
Roschelle, J., Rafanan, K., Bhanot, R., Estrella,
G., Penuel, B., Nussbaum, M., & Claro, S. (2010). Scaffolding
group explanation and feedback with handheld technology: Impact on
students’ mathematics learning. Educational Technology Research
and Development, 58 (4), 399-419.
Wenger , E. (1998) . Communities of practice:
Learning, meaning, and identity . Cambridge: Cambridge University
Press. |