數學問題解決是一個談了數十年（甚或更久）的課題，然而卻又歷久常新。常有人問，做數的量要多少才夠，甚或老師又會問，一課完了應給多少題作業。說句笑話，要看學生肯做多少題啊！（這當然是另一個複雜問題，牽涉着學生動機等等）。不過試想想，不同學校的學生（除了特殊的情況）做數的量應該是差不多的了。這個世界也不一定是有些甚麼秘密題庫、「黃崗密卷」之類、何以學生中有問題解決高手，亦有低手之分呢？除了天聰等各種因素外，問題的質可能比量來得更重要。Cronbach便指出：「計算743.2的開方不算是我們所考慮中的難題……學生只需依法泡製，並不比打字員把此稿件打出需要更多的工作。」關鍵是要看學生在解決問題過程中能否舉一反三、觸類旁通。為人津津樂道的「Pólya四部曲」便談到了「回顧」。這可以包括鼓勵學生多方面自我提問，如：答案正確嗎（不是指核對標準答案，而是自行驗算）？何以某方法可得出答案（原理）？答案中哪步最重要（關鍵）？答案可進一步簡化嗎？解答可否用於類似問題（推廣）？有其他答案嗎（一題多解）？若有其他答案，哪個較好，哪個較快，哪個能切合更廣的問題（有時快方法的適合性較窄）？有否資料不足或過多的情況（可惜大部分坊間題目都沒有這種情況）？若將題目條件改動又如何（觸類旁通）？等等。但現時不少學生做完數就算了，沒有分析問題解決規律，也沒有汲取解難題的教訓，如此不是會重複錯誤，便是做100題就只會100題（面對第101題好像又是從新解過），始終無法提升問題解決水平。

　　當然一些非常規題（如奧數題之類）有其功能與作用，但其實學生每天面對的習題已是大有可為。本文的主旨正是舉出一些這樣的例子。我們的做法是，首先只是在一些一般的學校裏搜集了最普通不過的數學測驗題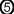，給學生做一做，抽出他們答得不太好的題目，並訪問他們的思路。針對這些思路的改進，問題解決能力就自然得到提升。

未能完全脫離直觀

　　先看以下一題（題1），很訝異地，這是較多同學做錯的。當然其中一個問題是圖中有隱藏資料：其中一邊知道是5 cm，要先找出另一邊也是5 cm才能繼續做下去。但這個錯誤分析仍屬表層；因為我們留意到不少學生都得出同一個10.125 c㎡的錯誤答案。在訪談之下，發覺原來這些做錯的學生都是直接用直尺量度邊長（4.5 cm），然後計算出面積來。其實這些學生不完全是錯的，因為有些題目確是要求學生用直接量度的方法去解題。

　　其中一個原因是他們把三角形的這個具體實物與具抽象性的「示意圖」混淆了。也顯示學生有可能未能完全從用直觀感知圖形過渡到三角形的這個「數學對象」。

資料不足的恐懼

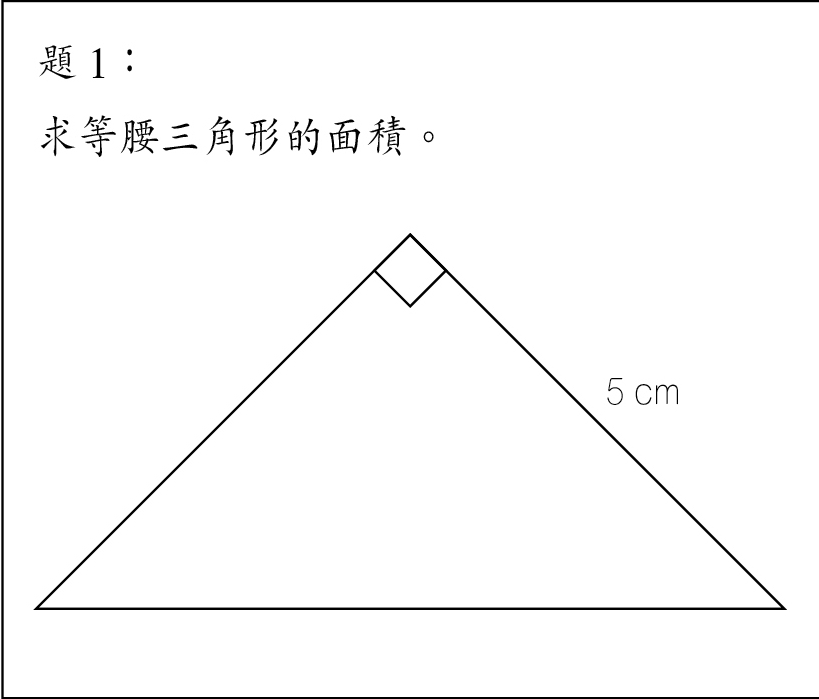
　　再看以下兩題，是關於面積的。題2比較複雜，但絕大部分學生均會做。因為用慣常的分割法和補足法就可以了。

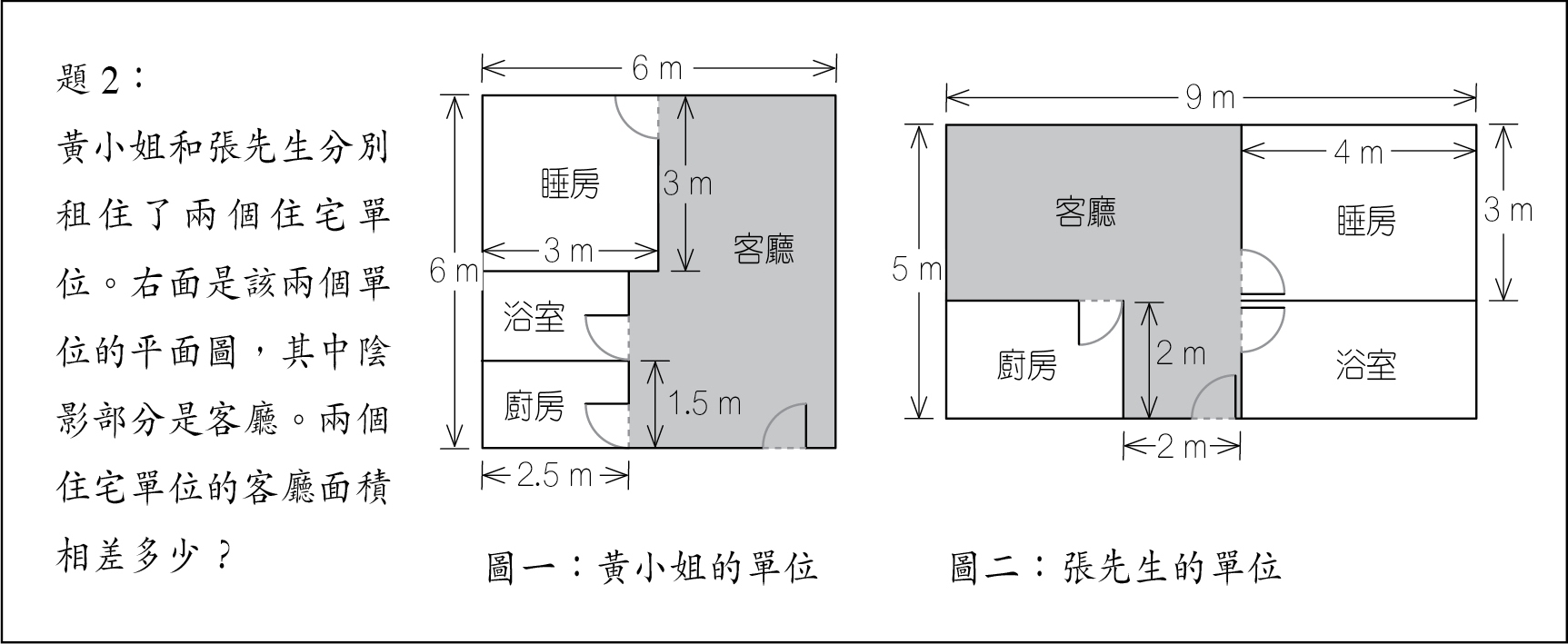
　　但不少學生卻做不了題3！

　　究其原因，是他們對題目中沒有提供一些邊的長度感到不安，而其實這些長度是不必知道的。在學生完成這題目時，可以指出A至E之位置原來沒有所謂。更可問學生：題目所給出的三個長度是否還有不必知道的呢？（「3厘米」是不必知道的）

關係圖

　　另一個較多學生答得不理想的是關於數量增減的題，如：

這一類型的題目一直延伸到百分比與百分比增減，其實用一些關係圖就可協助理解，如：

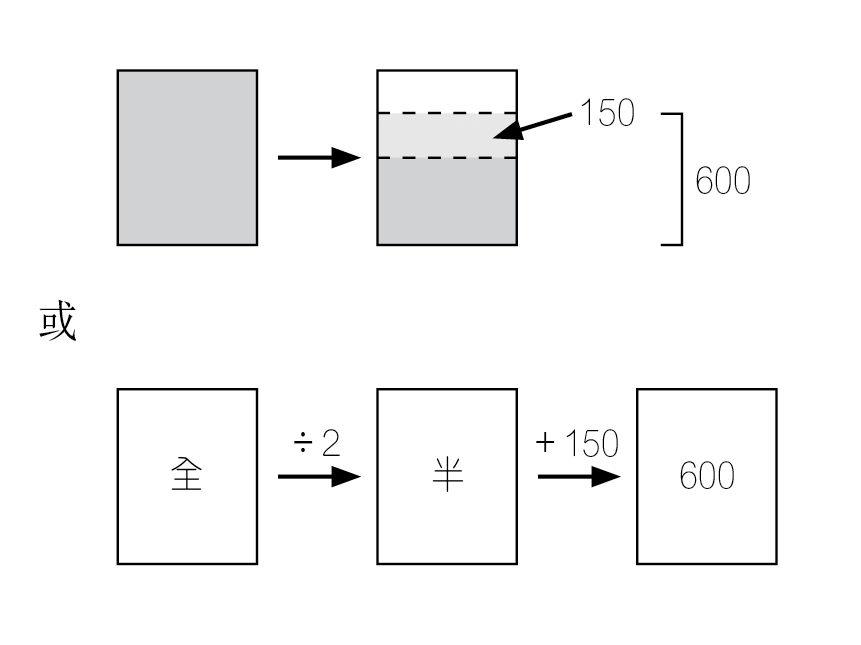
　　其實這個想法早在1978年已有所提出。這不只會讓學生把數學題解決得好一點，而且打開了關係性理解的可能。

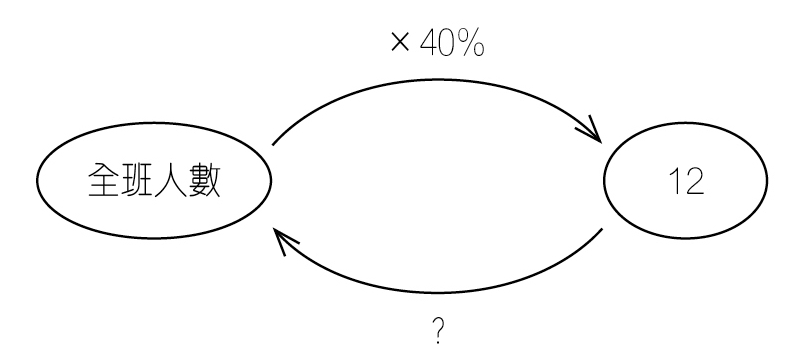
　　　　　　　　　　　　　　　　　　「箭頭圖」（來源：馮源，1978）

「全班30人中，男生佔60%，女生有幾人？」

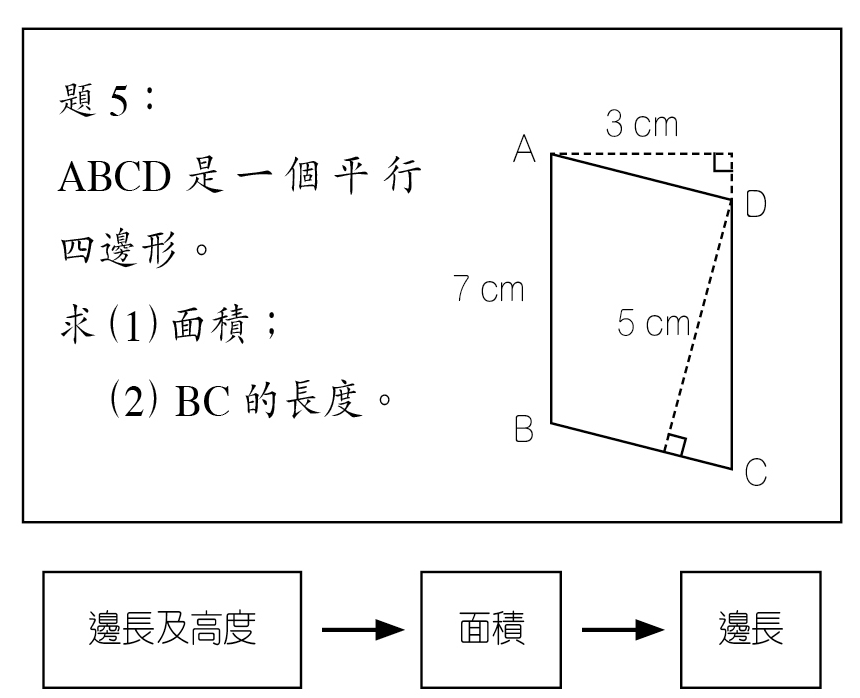
　　就算如以下的題目（題5），雖然不是上述的一類型，但其中牽涉到「次目標（sub-goal）之形成」，一個關係圖就能把思路整理得更好。

資料過多與不足

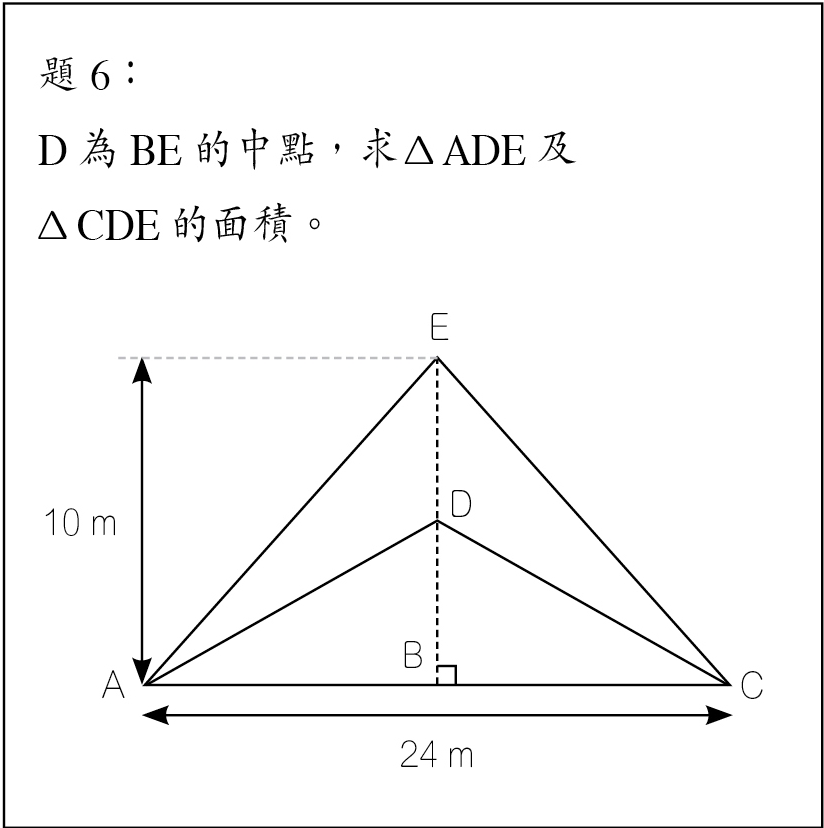
　　資料過多與不足是培養高層次思維能力不錯的手段9。這些亦可算是開放題的一種，上面的題3已可算是其中之一。我們在變式課程設計中也提出一些這樣的例子。題6亦是一道正常學校的測驗題，我們可以進一步的問：B的位置重要嗎？……

動動手、繼續探索

　　又有一題：

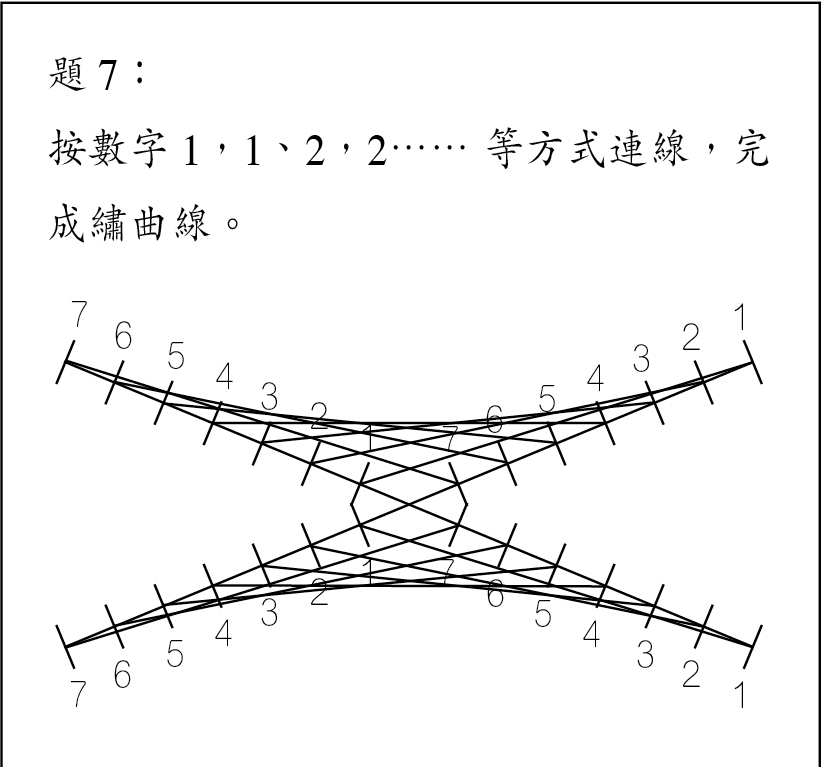
　　連接後，其實也可繼續探索這些規律。雖然繡曲線已不在基礎課程，其實在活動中動動也是好的。

　　不少人誤會這是雙曲線，其實它是拋物線。

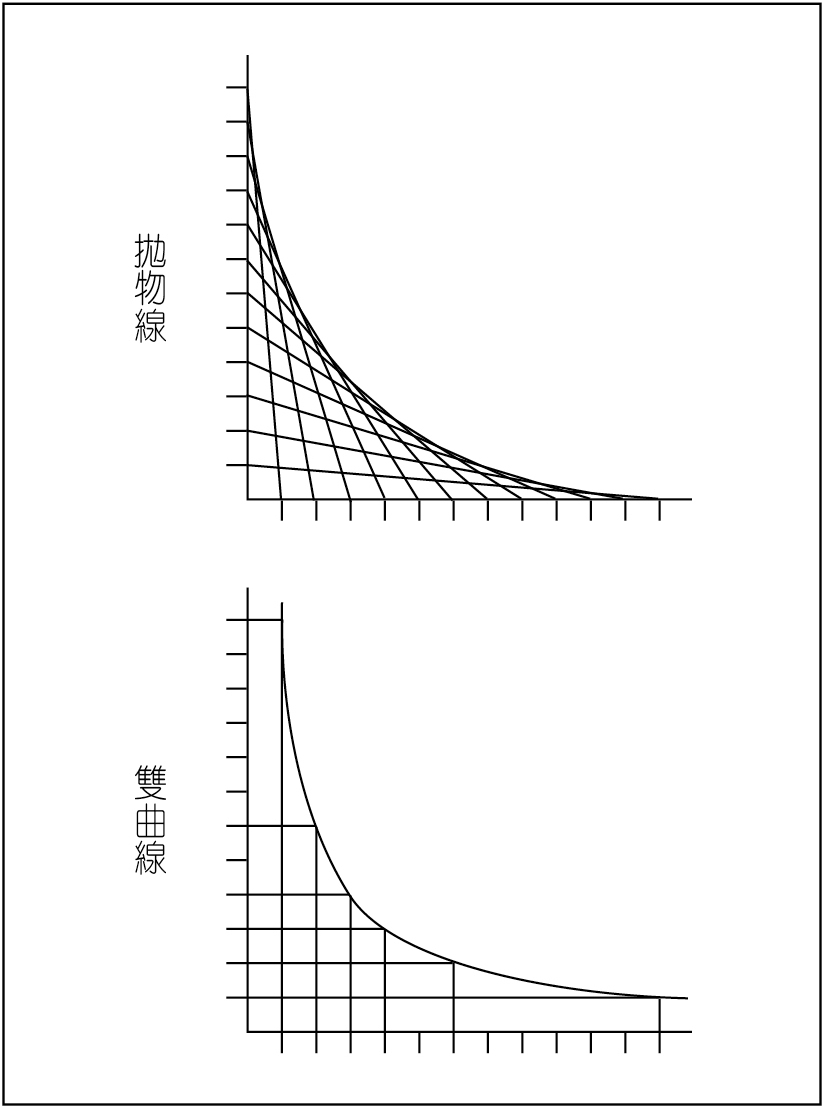
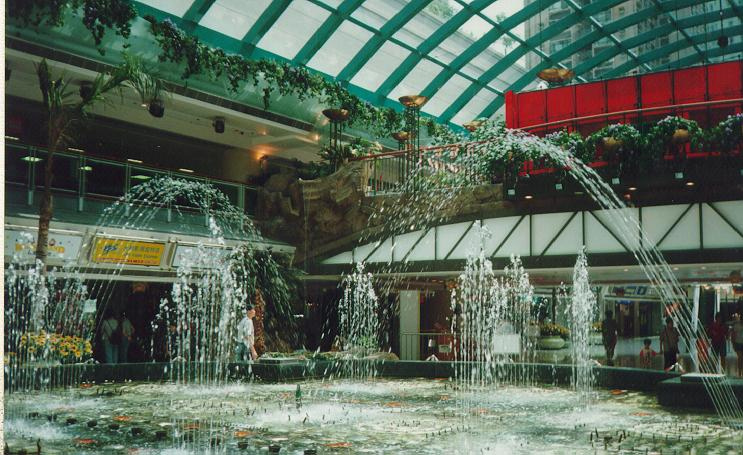
拋物線

結論

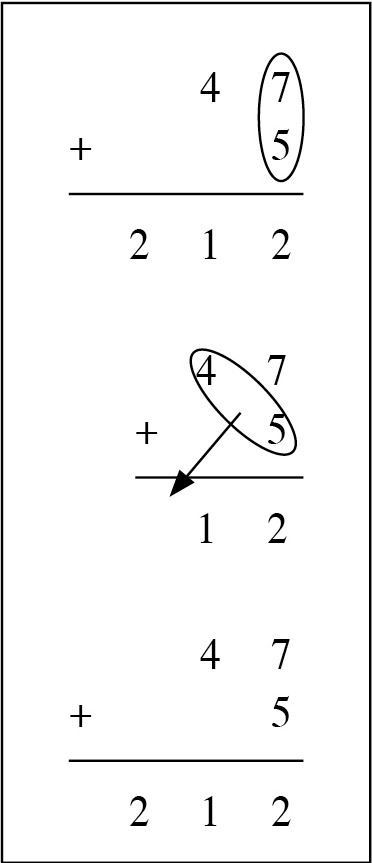
　　以上只是嘗試說明，只須用日常的習作，已能提升學生的問題解決能力。問題不只是題目的量，而是題目的質，和能否以數學問題診斷學生的思路。例如《數學教育實地觀察─II》提到如47 + 5 = 212的錯誤，用一句不小心就可解釋過去了。但其實有可能學生覺得7 + 5的12大「擁擠」了，於是把2擠出去了（以上是加法計算的情況，乘法計算的情況更常見）。所以老師應把學生的問題解決過程改變成學生思路顯示給老師的對話匣，學生的問題解決能力必定能夠提升。

　　最後謹以《斯蓋尼三氏解析幾何學》的中譯者序作結：「學習一般數學之要點，為方法、理論與思考，解析幾何學，亦然。方法為技術上問題，熟後方能生巧，此習題之所以不能不勤作也。理論為數學之精華，凡一定律或一定理當前，必須細究其理。是否全部明瞭？如若尚有疑點，必須時加應用。切不可徒事強記，以免食而不化。理論或應用題，須時加思考，務使觸類旁通，得心應手，方稱善讀。總之：天資雖有高下，成功端賴努力，更毋一暴十寒，則成績斐然，可預卜也。」

參考資料
	黃毅英（1990）。解題與數學教育。《數學傳播》54期，頁71-81。後載黃毅英（編）（1997）。《邁向大衆數學的數學教育》（頁59-82）。台北：九章出版社。
	黃崗本來是內地一個寂寂無名的城市，但高考成績特高，自此，很多內地補充練習均以「黃崗密卷」自居。
	Cronbach, I. F. (1955). The Meaning of problems. In J. M. Seidman (Ed), Readings in Educational Psychology (pp. 193 – 201). Boston, U.S.A.: Houghton Mifflin.
	Polya, G. (1945). How to Solve It. Princeton, U.S.A.: Princeton University Press.
	感謝有關學校提供試卷。
	馮源（1978）。如何打破應用題的難關。《今日的數學教學》，頁7-9。
	黃毅英（2001）。何不畫個表？《數學教育》13期，36-38。 黃毅英、林智中、孫旭花（2006）。《變式教學課程設計原理：數學課程改革的可能出路》。香港：香港中文大學教育學院香港教育研究所。 黃毅英（2007）。數學化過程與數學理解。《數學教育》25期，2-18。
	黃毅英（1990）。解題與數學教育。《數學傳播》54期，頁71-81。後載黃毅英（編）（1997）。《邁向大衆數學的數學教育》（頁59-82）。台北：九章出版社。
	Low, R., & Over, R. (1989). Detection of missing and irrelevant information within algebraic story problems. British Journal of Educational Psychology, 59, 296-305. 黃毅英（1996）。評核、擬題與數學教育。《數學傳播》80期，33-49。後載黃毅英（1997）（編）。《邁向大眾數學的數學教育》（頁153-184）。台北：九章出版社。
	黃毅英、林智中、孫旭花（2006）。《變式教學課程設計原理：數學課程改革的可能出路》。香港：香港中文大學教育學院香港教育研究所。
	黃毅英（2002）。《數學教育實地觀察 —— II》。香港：香港數學教育學會。
	Smith, P. F., Gale, A. S., & Neelley, J. H. (1912). New Analytic Geometry. London: Ginn. 〔Smith, P. F., Gale, A. S., & Neelley, J. H. (1978)。《斯蓋尼三氏解析幾何學》（邱調梅譯）。香港：中流出版社。〕