合作式的、討論型的課堂教學隨著教育改革的不斷深入而倍受教育界的有識之士重視,教學界從
1999 年秋季開始結合小學數學學科,探索了「開展『討論式』教學,激發學生創新意識」的研究。
討論式教學主要有同桌討論、小組討論、全班討論三種,本文將就作者推行小組討論教學的經驗作出分享。
小組討論式教學減少個別差異學習產生的問題
在教學過程中,學生的學習也受著同班同學的個別差異影響,因教師的教學進度要兼顧全班,對於吸收較慢的同學,老師總要花些時間教導他們,吸收較快的同學亦可能在等候教師「再教授」時產生不耐煩,若以小組式作探究討論學習,能力高的同學可在小組中協助能力稍遜的同學,一方面已學會了的同學不用花時間「等」別人學習,而是協助未學會的同學,使兩者皆有收穫;另一方面,能力稍遜的同學有時亦能提出一些探究問題的點子,讓同組同學一起討論。
討論式教學激發學生作探究式學習的課堂例子
維果茨基(Vygotsky)在其社會建構論中提出的最近發展區理念,提出學生在已有既定知識上,若得到幫助與輔導,便能發展下一區域,以鷹架作用的配合,便能促成學生的學習,意思是給學生進行探究的問題,是學生未知的知識,但學生能用已有知識去建構及解決的,以下舉一個本人於課堂中曾用的例子:
教授六年級數型(奇數之和──正方形數)
1 + 3 + 5 + 7 + 9 + …
+ 99 + 101 = ?
先著同學分為 4
人一組,給予他們以下問題一起討論:
1. 1 + 3 + 5
2. 1 + 3 + 5 + 7 = ?
3. 1 + 3 + 5 + 7 + 9 = ?
4. 1 + 3 + 5 + 7 + 9 +
… + 13 + 15 = ?
5. 1 + 3 + 5 + 7 + 9 +
… + 19 + 21 = ?
6. 1 + 3 + 5 + 7 + 9 +
… + 99 + 101 =
?
六年級同學基本上會計算加法,分組後同學很快計算到 1-4
題的答案,教師再到每組「聆聽」及提問,引導每組同學作探究。引導問題按各組情況提出: 進度較慢組別:
| 1. |
第 1-4
題計算出的答案有甚麼特別 ?(平方數) |
| 2. |
第 5
題的答案你們想與上題的有何共通之處 ?(都是平方數) |
| 3. |
第 5
題的答案是多少 ? (64) |
| 4. |
試計算第 6
題,差甚麼資料便可計算答案?(第幾個平方數) |
| 5. |
再看第 1-5
題,答案與式子跟第幾個平方數有何關係 ? (有多少項便是第幾個平方數) |
| 6. |
可知 1-101
有多少項 ? |
| 7. |
若 2,4,6,8,10,12…20
有多少項 ? (10) |
| 8. |
1,3,5,7
+ …
21 有多少項 ? (10)能計算出來嗎?〔(21
+ 1) ÷ 2〕 (11) |
| 9. |
1,3,5,7
+ …
21 有多少項 ? 〔(101
+ 1) ÷ 2 = 51〕 |
| 10. |
1 + 3 + 5 + 7 + 9 + … +
99 + 101 = ? (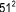 =
2601)
=
2601) |
進度較快組可只問第 6,7
題,同學自己探究出項數的計算方法,便會計算連續奇數之和,接著便要各組想出解釋,可給予同學一些豆讓同學排列探究,不同組別可能出現不同排列方法,著他們按式子及答案排列,然後請同學解釋為何奇數之和是平方數,再引入「正方形數」名稱,由學生的發現導入計算的方法,最後出示正方形數題目讓學生做,檢視教學成效。
進行討論教學注意事項
| 1. |
|
教師於整個教學過程需作以下七個步驟,前提準備→質疑導入→新知展示→精講點撥→鞏固新知→課堂小結→目標檢測。 |
| 2. |
|
採用小組討論教學需配合適用的課題,需依據學生的年齡特徵和水平而設計,具探索性和開放性,能給學生提供自主探索的機會,讓學生從觀察、操作、討論、交流、猜測、歸納、分析和整理的過程中,理解數學問題的提出、數學概念的形成和數學結論的獲得,以及數學知識的應用。 |
| 3. |
|
在小組教學中,要使每個學生充分參與課堂討論,教師於課堂中要多鼓勵每組同學都於小組中發言分享,可透過向全班讚賞討論認真的組別,增進討論氣氛。 |
| 4. |
|
在同學討論時,教師須到每組聆聽及參與討論,並對討論過程進行指導與調控,作出必要的提示、點撥、設疑和答疑。 |
| 5. |
|
營造寬鬆的討論氣氛,多讚賞,心理學家羅傑斯提出:「有利於創造活動的一般條件是心理的安全和心理的自由。從本質上講,創造性活動必定是異樣的,從而必定是異常的行為。對一個人的表揚讚許乃是促進心理安全的重要因素之一。當一個人在心理上感到安全時,他就不會害怕表現和發展他的發散思維和求異思維,他可以在進行發散思維時無須處於防禦狀態,從而保持心理的自由。」 |
| 6. |
|
教師要尊重學生的創造性,多鼓勵,有時同一題目會有不同解決方法,學生提出的意見需細心聆聽。 |
| 7. |
|
教師不是唯一的評價者,不能對學生不適當的回答進行否定,而是進一步提問進行引導,要重視討論的過程而不是討論的結果。 |
| 8. |
|
問題的關鍵處就是討論點,解決一個數學問題往往有些「突破口」,這個突破口就是解決問題的關鍵,教師在引導提問時宜找緊討論,避免學生遠離問題。 |
課後回顧
整堂教學佷流暢,學生大部分積極參與討論,當學生自己「發現」了規律計算,他們均非常雀躍,亦見他們增強了對學習數學的自信心,唯教師太著重前面的討論,忽略了後部鞏固工作,令部份學生未能即時將此題形深化成普通題目,這是再教授此課時應注意的地方。 |