| 圖形面積的計算首要是要熟記各種規則圖形的面積計算公式,如正方形、長方形、三角形、平行四邊形、梯形、圓形及扇形等,然後再運用不同的解題方法尋找不規則圖形的面積。尋找圖形面積的方法有多種,在這份論文中,我會詳述如何讓學生運用加減法求圖形的面積。
運用加減法求面積的重點
一般的平面圖形是不規則的,但大多數都是由一些規則圖形拼合組成的,而運用加減法求面積是根據圖形組合的形式,轉化成規則圖形的和差關係,用求幾個圖形的面積和或是差的方式來求組合成圖形的面積,其解題關鍵是在於弄清題目的必要條件,找出圖形組合間的和或差的關係,從而找出解題的突破點。
運用加減法求面積的難點
學生運用加減法求圖形面積的難點是在於他們不能找出圖形組合中和或差的關係,因而不能找出解題的關鍵而感到無從入手。
運用加減法求面積的教學法
一、加法
對於某些圖形組合,由於它們一般是由一些不同的圖形組合而成,因此我們可以指導學生小心觀察圖形組合,從中找出該圖形組合是由哪些規則圖形組成的,然後逐一找出每個構成該圖形組合的構成部分,最後把這些構成部分相加起來,便能求出整個圖形組合的面積,以下舉一例子加以說明:
正方形
ABCD 的邊長為 1 厘米,依次以
A、B、C、D 為圓心,以 AD、BE、CF、DG
為半徑畫出扇形,求陰影部分的面積。(取 π=
3.14)
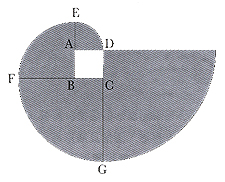
在解這道題時,我們可以引導學生從圖中找出陰影部分其實是由四個扇形組成的,只要我們求出這四個扇形面積的和,便能找出陰影部分的面積,從題中很容易便可以看出四個扇形的半徑依次為:
AD
= 1 厘米
BE = 1 + 1 = 2(厘米)
CF = 1 + 2 = 3(厘米)
DG = 1 + 3 = 4(厘米)
要求陰影部分的面積即是求四個半徑各不相同的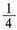 圓的面積和: 圓的面積和:
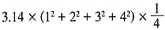
= 23.55(平方厘米)
二、減法
對於某些圖形組合而言,我們可以用圖形組合間的差的關係來解題,即是求該圖形組合中某一個圖形與另一個圖形的面積之差,從而找出題目中指定部分的面積,以下舉一例子加以說明:
求圖中陰影部分的面積。(取 π= 3.14)
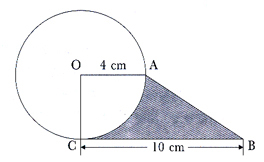
對於這道題,我們可以引導學生先觀察圖形,發現直接求圖中陰影部分的面積是困難的,留意圖形的特點,梯形
OABC、扇形
AOC 的面積易求,因此用梯形的面積減去扇形的面積便可求出陰影部分的面積:

三、二次求差法
有時對於一些圖形組合,我們要重複運用圖形組合間的差的關係來解題才能找出題目中指定部分的面積,這種方法稱為二次求差法,即是說如要求出某陰影部分的面積,我們不能從圖形組合減去某一部分而直接求得,而是要運用組合圖形間差的關係,先找出某一組成部分的面積,然後再次運用組合圖形間的差的關係找出題目中要求陰影部分的面積,現舉一例子加以說明:
圖中長方形 ABCD
的 AB = 6 厘米、BC
= 4 厘米,求陰影部分的面積。(取 π=
3.14)
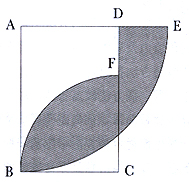
從圖中可以看出,陰影部分面積等於扇形 BAE
的面積減去空白部分 ABFD
的面積,ABFD 是一個不規則圖形,它的面積無法直接求出,我們便要先用長方形
ABCD 的面積減去扇形 BCF
的面積,求出 ABFD 的面積,然後才用扇形
BAE 的面積減去 ABFD
的面積,求得陰影部分的面積,這樣通過二次求差法便求得陰影部分的面積了。
空白部分 ABFD
的面積為:
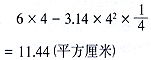
陰影部分的面積為:
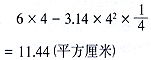
學生較易掌握加法和減法求面積
從我的實際教學經驗中,我觀察到一般同學在解答圖形面積的問題時,都能掌握運用加法或減法求圖形的面積。
但對於運用二次求差法求圖形面積,同學們會感到稍困難,由於運用二次求差法解題的圖形組合一般較複雜,學生不易看出圖形組合間差的關係,而且運用兩次求差法才能求出某圖形面積,增加了解題的難度;另一原因是學生的圖形與空間感往往是在數學範疇中較弱的一個範疇,他們欠缺空間感及想像力,以致不能從圖中看出圖形組合間的關係而感到困難,因此對學生而言,二次求差法較難運用。
協助學生解決圖形面積困難的策略
我認為針對上述同學們在解決圖形面積所面對的困難,老師可以運用一些課堂活動或策略來協助同學找出圖形的面積。首先,老師可以讓學生運用不同規則圖形的透明膠片自由拼砌成圖形組合,增加學生的圖形與空間感,然後著同學一起研究如何求出該圖形組合或是其中某一指定部分的面積,這樣透過同學們親自動手做的活動,一方面使他們更具體明白圖形組合間的關係,而另一方面又可以增加他們的學習興趣。計算不再局限於紙筆上,而可以動手做,同學們會更感興趣,再者,同學們可以比賽形式解題,由一組同學負責拼砌圖形組合,而另一組同學則負責求圖形面積,以增加活動的刺激性。
除了動手拼砌圖形組合外,我們亦可以讓學生在紙上自擬圖形組合,然後讓其他同學解題,並以比賽形式進行,同樣亦能提升學生的圖形與空間感,增加思考機會。
此外,多做不同類型的題目也是提升圖形與空間感的方法之一,老師應揀選不同類型的題目給學生多練習,增加他們的思考機會,而在解題時,老師可鼓勵學生在圖形上加上適當的線段,使他們更易分辨出圖形組合中的組成部分,使解題思路更具體及清晰,更易找出圖形組合中和或差的關係,這是解題時的一些技巧。
總結
其實,在解答圖形面積的題目時,有很多種不同的方法,對於某些題目,我們除了可以運用本論文所述的加法和減法外,亦可以運用其他解題方法,例如割補法、旋轉平移法、加添輔助線、利用方程等,但在這裡本人不詳述這些方法了。老師在教導圖形面積時,應鼓勵學生用不同的方法解答同一道題目,不需要局限於老師在課堂上所提供的方法,這樣才能發展學生的創造力及思維能力。而老師在羅列了各同學的解題方法後,可與學生一起分析在眾多方法中,哪一個方法較為省時、較少機會出錯、計算步驟較簡單等,從而發展學生的分析能力,使學生能從眾多方法中挑選一種最適合的方法解題,我認為這點是非常重要的。學習數學,並不是死記硬背公式或方法,而是靈活運用不同的方法解題,發展他們的思維及分析能力,使他們終生受用,這樣才是學習數學的最大意義。 |